
Dem Self-Attention-Mechanismus unter die Haube geschaut!#
Das Ziel von Self-Attention ist es, die wechselseitigen Abhängigkeiten zwischen Tokens im Satzkontext zu erkennen und zu gewichten.
Für jedes einzelne Token wird dabei ein neues kontextangepasstes Embedding berechnet – also ein neuer Merkmalsvektor, der die gewichteten Informationen aller Tokens bis zum aktuellen Token im Satz berücksichtigt.
So entsteht für jedes Token eine neue Repräsentation, die seine Bedeutung im Kontext der anderen Tokens widerspiegelt.

Jedes Token startet mit einem eigenen Embedding aus der Roh-Embedding-Lookup-Tabelle – sie wird während des Trainings gelernt und bleibt bei der Inferenz unverändert. So kann etwa „zwei“ als Zahl, „schwarze“ als Farbe und „Katzen“ als Tier dargestellt werden.
Durch den Transformer-Mechanismus werden diese Informationen gemeinsam verarbeitet. Dadurch erhält das Token „Katzen“ ein neues, kontextangepasstes Embedding, das die Bedeutung des gesamten Satzes widerspiegelt – das Bild zweier schwarzer Katzen. (Reale Embeddings sind natürlich latent, wie wir bereits gesehen haben.)
Ein Transformer führt eine große Menge an Berechnungen durch – und das gleichzeitig für viele Tokens. Um all diese Berechnungen – von den Q/K/V-Transformationen bis zur Gewichtung der Kontextinformationen – effizient durchzuführen, braucht es ein Werkzeug, das viele Operationen parallel und blitzschnell ausführen kann.
➔ Hier kommen Matrizen ins Spiel …
Mathe? Keine Sorge!#
Um Self-Attention richtig zu verstehen, brauchen wir etwas Mathe – aber keine Angst, das ist handlich und intuitiv.
Die zwei wichtigsten Werkzeuge sind:
Vektoren: Listen von Zahlen (kennen wir bereits)
[0.3, -1.2, 4.7, ...]
Matrizen: Tabellen aus Zahlen – sie ermöglichen schnelle, parallele Berechnungen
[ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
Warum Matrizen?#
Die bahnbrechende Publikation von Vaswani et al. („Attention is All You Need“) hat nicht nur eine revolutionäre Architektur vorgestellt, sondern sie auch vollständig auf Matrizenoperationen aufgebaut.
Dieser Ansatz bildet bis heute das Herzstück moderner Transformer-Modelle – darunter GPT, Claude, Gemini, Granite und viele andere.
Die Rechenstruktur wurde seitdem nur leicht optimiert, die Grundidee ist aber nahezu unverändert übernommen worden.
Warum Matrizen so mächtig sind#
Matrizen haben zwei entscheidende Vorteile:
- Sie ermöglichen es, Millionen mathematische Operationen in einem Schritt durchzuführen – dank hochoptimierter Matrixmultiplikation.
- Sie lassen sich hervorragend auf GPUs parallelisieren – was sie ultra schnell macht.
Matrizen werden schon seit Jahrzehnten in der Computergrafik eingesetzt – besonders in einem Bereich, den fast jeder kennt: 3D-Spiele.
In den letzten Jahren ist die Qualität und der Realismus in Games regelrecht explodiert.
Hauptgrund dafür: Grafikkarten (GPUs) wurden immer leistungsfähiger und können Millionen von Vektor- und Matrizenberechnungen pro Sekunde durchführen.
Man könnte sagen: Power-Gamer haben den Weg bereitet, damit heutige Computer zu echten Matrizenspezialisten geworden sind – eine Entwicklung, von der KI-Modelle heute massiv profitieren.
Erlebe Matrizen in Aktion!#
In dieser 3D-Szene siehst du ein Raumschiff als anschauliches Beispiel.
Eine Matrix genügt
Anstatt jeden Rechenschritt – wie Verschiebung, Rotation (um X-, Y- und Z-Achse), Skalierung usw. – einzeln auszuführen, wird das gesamte Modell inklusive Umgebung mit einer einzigen sogenannten Model-View-Projection-Matrix (MVP) transformiert.
Verschiedene Blickwinkel
Du kannst das Raumschiff dabei aus unterschiedlichen Perspektiven betrachten – ähnlich wie wir das später bei Transformationen der Embeddings machen, um Informationen gezielt aus verschiedenen Blickwinkeln zu erfassen.
👉 Probiere es aus: Du kannst dich mit der Maus oder Touch in der Szene frei bewegen!
- linke Maustaste: drehen,
- rechte Maustaste: verschieben,
- Scrollrad: zoomen.
Drei verschiedene Ansichten von jedem Token#
Jedes Token liegt ursprünglich als Embedding-Vektor vor – ein Vektor mit z. B. 12.288 Zahlen, die seine Bedeutung in einem hochdimensionalen Raum abbilden.
Aus diesem Embedding-Vektor werden durch Projektion drei neue Vektoren gebildet, die im Attention-Mechanismus unterschiedliche Funktionen erfüllen:
- ❓ Query (Q) Vektor – der mit den Keys der anderen Tokens auf Ähnlichkeit geprüft wird
- 🔐 Key (K) Vektor – der als Grundlage für diesen Vergleich dient
- 📦 Value (V) Vektor – dessen Inhalte – je nach Relevanz – in die neue Darstellung des Tokens einfließen

Die Transformation erfolgt durch drei verschiedene – beim Training mit Milliarden Wörtern erlernte – Gewichtsmatrizen:
Eine für Query, eine für Key, eine für Value.
Kurzer Exkurs zur Multiplikation von Matrizen und Vektoren:
Multiplizierst du einen Vektor mit einer Matrix, dann gehst du Spalte für Spalte durch die Matrix: Du multiplizierst jedes Element des Vektors mit dem Element derselben Zeile in dieser Spalte, addierst die Produkte – und diese Summen sind die Einträge des neuen Vektors.
Die Länge des Vektors muss mit der Anzahl der Zeilen der Matrix übereinstimmen.
Die Rechenschritte sind einfach – ich habe sie dir hier aufgeschrieben:$$ \vec{v} \cdot W = \begin{bmatrix} \color{blue}{2} & \color{red}{3} & \color{green}{1} & \color{orange}{1} \end{bmatrix} \cdot \begin{bmatrix} \color{blue}{1} & \color{blue}{0} & \color{blue}{2} \\ \color{red}{2} & \color{red}{1} & \color{red}{1} \\ \color{green}{0} & \color{green}{1} & \color{green}{0} \\ \color{orange}{1} & \color{orange}{0} & \color{orange}{1} \end{bmatrix}= \begin{bmatrix} \color{blue}{9} & \color{red}{4} & \color{green}{8} \end{bmatrix} $$
$$ \color{blue}{2} \cdot \color{blue}{1} + \color{red}{3} \cdot \color{red}{2} + \color{green}{1} \cdot \color{green}{0} + \color{orange}{1} \cdot \color{orange}{1} = 2 + 6 + 0 + 1 = \color{blue}{9} $$ $$ \color{blue}{2} \cdot \color{blue}{0} + \color{red}{3} \cdot \color{red}{1} + \color{green}{1} \cdot \color{green}{1} + \color{orange}{1} \cdot \color{orange}{0} = 0 + 3 + 1 + 0 = \color{red}{4} $$ $$ \color{blue}{2} \cdot \color{blue}{2} + \color{red}{3} \cdot \color{red}{1} + \color{green}{1} \cdot \color{green}{0} + \color{orange}{1} \cdot \color{orange}{1} = 4 + 3 + 0 + 1 = \color{green}{8} $$
Für jedes Token wird das ursprüngliche Embedding x_i mit den drei Gewichtsmatrizen
W_Q, W_K und W_V multipliziert, um die drei Vektoren Query (Q), Key (K) und Value (V) zu erzeugen.
Diese bilden die Grundlage für den Self-Attention-Mechanismus – vollständig auf Matrizenoperationen basierend und dadurch sehr effizient.
In der Praxis kommt ein weiterer Vorteil hinzu: Alle Tokens der Eingabesequenz X werden parallel verarbeitet – über eine einzige Matrixmultiplikation, bei der jede Zeile einem Token entspricht.
$$ \begin{aligned} \mathbf{Q} &= \mathbf{X} \cdot \mathbf{W}^Q \\ \mathbf{K} &= \mathbf{X} \cdot \mathbf{W}^K \\ \mathbf{V} &= \mathbf{X} \cdot \mathbf{W}^V \end{aligned} $$
Die Gewichtsmatrizen haben so viele Zeilen wie das Embedding Dimensionen besitzt (z. B. 12.288) und so viele Spalten wie die gewünschte Zieldimension vorgibt (z. B. 128).
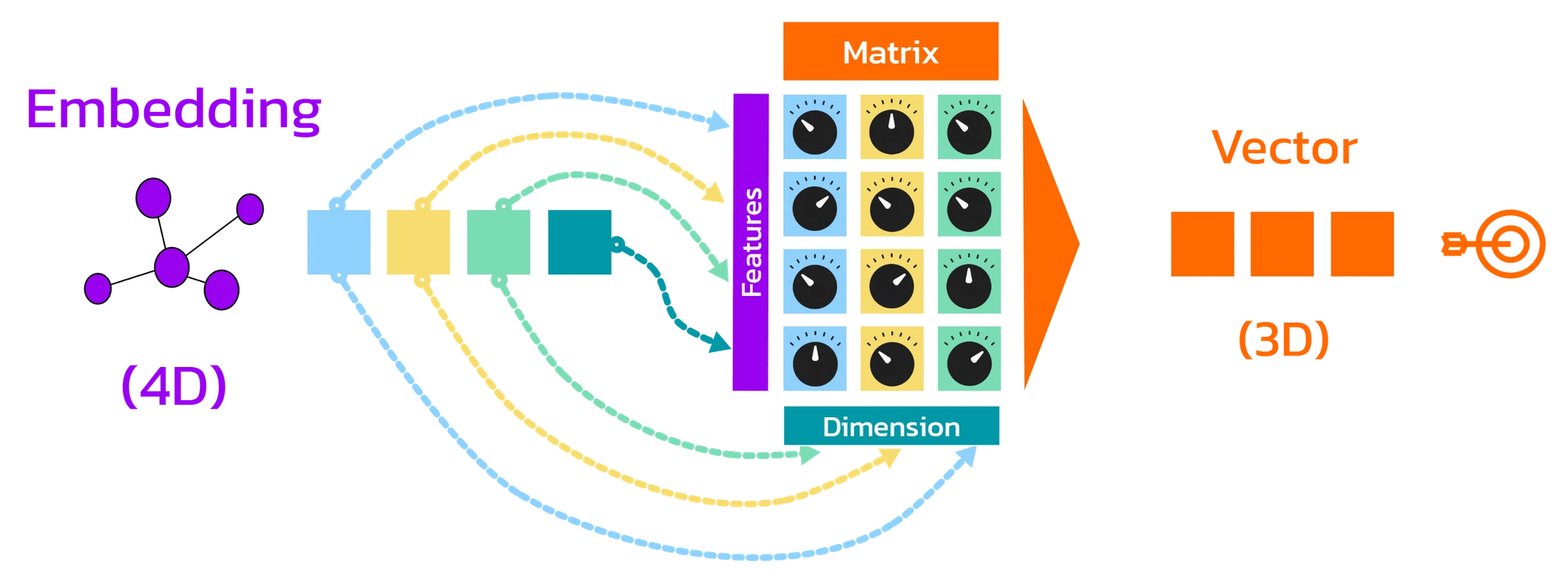
Das Embedding wird mit jeder Spalte der Gewichtsmatrix elementweise multipliziert und die Produkte addiert:
- Die erste Spalte liefert das erste neue Merkmal,
- die zweite Spalte das zweite neue Merkmal,
- und so weiter …
Jedes dieser neuen Merkmale entsteht durch eine lineare Projektion der ursprünglichen Merkmale – einige werden dabei verstärkt, andere abgeschwächt, manche vollständig ausgeblendet oder sogar umgekehrt (negiert).
Auf diese Weise entsteht aus dem ursprünglichen Merkmalsvektor eine neue Repräsentation in einem kompakteren, reduzierten Merkmalsraum – zum Beispiel von 12.288 auf 128 Merkmale.
Wichtig nochmals zu erwähnen!#
- Alle Tokens verwenden dieselben Q-, K- und V-Matrizen pro Attention-Head.
Es gibt also keine token-spezifischen Gewichtungen, sondern eine einheitliche Transformation für alle Eingaben – das sorgt für maximale Effizienz und Generalisierung. - Die Q-, K- und V-Matrizen sind unabhängig voneinander.
Sie lassen sich nicht voneinander ableiten oder direkt in Beziehung setzen – jede von ihnen hat eigene Parameter, die ausschließlich durch das Training gelernt wurden. - Mit einer solchen Q/K/V-Projektion kann das Modell jeweils nur eine bestimmte Art semantischer Beziehung zwischen Tokens erfassen.
Ein einzelner Attention-Head bildet dabei typischerweise genau eine Perspektive ab – z. B. „welches Subjekt gehört zu welchem Verb?“. - In einem vollständigen Transformer-Modell arbeiten jedoch mehrere Heads gleichzeitig und in mehreren gestapelten Layern.
So entstehen tausende Projektionen, die gemeinsam eine Vielzahl semantischer Muster und Abhängigkeiten erfassen – vom Satzbau bis zur Bedeutung über ganze Absätze hinweg – mehr dazu in einem späteren Abschnitt.
Warum wird die Dimension reduziert?#
- Die Reduktion spart Rechenzeit und Speicher – besonders bei großer Kontextgröße,
da die Berechnungen im Attention-Mechanismus quadratisch mit der Anzahl der Tokens zunehmen. - Sie erlaubt es dem Modell, die Informationen in einer kompakteren Form darzustellen –
jeder sogenannte Attention-Kopf arbeitet dadurch mit einer eigenen Projektion, die bestimmte Aspekte der ursprünglichen Merkmale hervorheben kann. - Der Transformer verwendet mehrere solcher Attention-Köpfe.
Damit jeder Kopf effizient arbeiten kann, wird die ursprüngliche Embedding-Dimension aufgeteilt – z. B. bei 96 Köpfen: 12.288 / 96 = 128 Dimensionen pro Kopf.
👉 In dieser interaktiven Demo wird das Prinzip anschaulich visualisiert#
Wie entstehen diese Q,K,V Matrizen?#
Die Q-, K- und V-Matrizen werden durch Training mit riesigen Textmengen gelernt – meist Milliarden von Wörtern.
Das Trainingsziel ist immer die Vorhersage des nächsten Tokens -> Fehlerhafte Vorhersagen führen zu Rückmeldungen über Backpropagation.Dadurch lernen die Matrizen:
- Query- und Key-Vektoren so anzupassen, dass relevante Tokens hohe Ähnlichkeit zueinander aufweisen
- Value-Vektoren so zu gestalten, dass nur kontextrelevante Informationen weitergegeben werden
So erkennt der Transformer, welche Tokens relevant füreinander sind#
Im Kapitel über Embeddings haben wir bereits gesehen, dass semantisch ähnliche Tokens im Merkmalsraum näher beieinander liegen.

Die Nähe zweier Vektoren wird entweder über ihren Abstand oder den Winkel zwischen ihnen gemessen – bei manchen Verfahren spielt auch ihre Länge eine Rolle.
Bei Transformern spielt vor allem der Winkel zwischen den Vektoren eine zentrale Rolle – nicht ihr euklidischer Abstand.
Zur Erinnerung: Es gibt zwei gängige Verfahren, um Ähnlichkeit über Winkel zu messen:
Skalares Produkt (Dot-Produkt)
Hier werden die entsprechenden Komponenten zweier Vektoren multipliziert und anschließend aufsummiert.
Das Ergebnis ist ein einzelner Wert, der die semantische Ähnlichkeit ausdrückt:
- nahe 0 → kaum Ähnlichkeit
- positiv → semantisch ähnlich
- negativ → eher gegensätzlich
$$ \mathbf{x} \cdot \mathbf{y} = \sum_{i=1}^{n} x_i , y_i $$
Kosinus-Ähnlichkeit
Die Kosinus-Ähnlichkeit ist ein normalisiertes Skalarprodukt.
Sie berücksichtigt nur den Winkel zwischen den Vektoren – unabhängig von ihrer Länge.
Das Ergebnis liegt immer zwischen –1 und 1.
$$ \cos(\theta) = \frac{ \vec{A} \cdot \vec{B} }{ | \vec{A} | \cdot | \vec{B} | } $$
| Wert | Bedeutung |
|---|---|
| +1 | exakt gleiche Richtung |
| 0 | orthogonal → keine Ähnlichkeit |
| −1 | exakt entgegengesetzt |
Attention Attention!#
Bei Transformern ist entscheidend, welche Tokens Einfluss aufeinander ausüben.
Genauer: Für jedes einzelne Token zählt, wie relevant die anderen Tokens für es sind – also welche Informationen sie beisteuern können, die zu seiner Repräsentation im Kontext beitragen.
Um diese Relevanz zu berechnen, haben wir die Tokens bereits mithilfe der Gewichtsmatrizen unterschiedlich projiziert:
Einmal als Query-Vektor und einmal als Key-/Value-Vektoren.
Je besser die ❓Query eines Tokens zu den 🔐Keys der anderen passt, desto mehr 📦Value wird von diesen Tokens übernommen.
Attention Score#
Die Berechnung der Aufmerksamkeit zwischen Tokens bezeichnet man als Attention Score.
Dabei geht es nicht um einen klassischen geometrischen Abstand, sondern um ein Maß für ihre Nähe im Merkmalsraum – zum Beispiel über die Kosinus-Ähnlichkeit.
Vaswani et al. entschieden sich für die pragmatische Lösung, die besonders effizient ist:
Statt die aufwändige Kosinus-Ähnlichkeit mit zusätzlicher Normierung zu berechnen,
verwenden sie direkt das Skalarprodukt (Dot-Produkt):
$$ \text{score} = \mathbf{q} \cdot \mathbf{k}^\top $$
Das Dot-Produkt hat noch einen weiteren Vorteil:
Beim Dot-Produkt tragen sowohl der Winkel zwischen den Vektoren als auch ihre Länge zum Ergebnis bei.
Damit hat das Modell die Freiheit, sowohl die Richtung (semantische Nähe) als auch die Stärke einzelner Merkmale (Vektorlängen) zu berücksichtigen.
Allerdings ergibt sich nun ein kleines Problem:
Skalarprodukte in hochdimensionalen Räumen können sehr große Werte annehmen.
Das erschwert die spätere Gewichtung, weil einzelne Tokens dadurch übermäßig stark hervorgehoben werden, während andere kaum noch berücksichtigt würden.
Die Lösung ist einfach und effizient:
Man teilt das Ergebnis durch die Wurzel der Dimensionalität des Key-Vektors (√dk).
So bleiben die Scores stabil und vergleichbar:
$$ \text{score} = \frac{\mathbf{q} \cdot \mathbf{k}^\top}{\sqrt{d_k}} $$
👉 Token-Relevanz: Probiere aus, wie sich Winkel und Dimensionen auf Cosine Similarity und Dot-Produkt auswirken#
Was bedeutet das T bei den Keys?
Das ‚T‘ steht für Transponieren: Es macht aus dem Key-Zeilenvektor einen Spaltenvektor, sodass das Skalarprodukt mit dem Query-Zeilenvektor berechnet werden kann.
Die Attention Score Matrix#
Jetzt berechnen wir diese Scores für alle möglichen Kombinationen von Tokens im Satzkontext.
Dazu erstellen wir eine Tabelle: Alle Tokens stehen sowohl in den Zeilen (als Query) als auch in den Spalten (als Key).
An jedem Schnittpunkt wird das Skalarprodukt zwischen Query- und Key-Vektor berechnet – das ergibt den Attention Score.
So entsteht eine vollständige Attention-Matrix, die zeigt, wie stark jedes Token auf alle anderen achtet.(In dieser Attention-Matrix treten nur positive Scores auf, obwohl negative ebenfalls möglich wären.)
Die Attention-Score-Matrix ist konzeptionell von Größe n × n. Der Rechenaufwand wächst damit quadratisch mit der Länge des Kontextfensters, und bei “naiver” Implementierung gilt dies auch für den Speicherbedarf.
Bei mehreren tausend Tokens steigen die benötigten Ressourcen entsprechend stark an und stellen heutige Hardware schnell vor praktische Grenzen. Ohne spezielle Optimierungen lassen sich in der Praxis meist nur einige Tausend Tokens effizient verarbeiten.
Sehr große Kontextfenster im Bereich von 100.000 Tokens und mehr sind technisch möglich, erfordern jedoch optimierte Verfahren wie FlashAttention sowie teilweise zusätzliche strukturelle Ansätze wie Sparse Attention oder Segmentierung.
Ein weiterer limitierender Faktor ist die Attention selbst – bei sehr langen Kontexten kann sich der Fokus so stark verteilen, dass wichtige Stellen an Gewicht verlieren.
In der Praxis werden die Attention-Scores als skaliertes Matrixprodukt der Query-Matrix mit der transponierten Key-Matrix berechnet. Moderne Implementierungen wie FlashAttention führen diese Berechnung blockweise (tiled) aus und vermeiden dabei, die vollständige n × n-Score-Matrix im Speicher abzulegen. $$ \text{score} = \frac{\mathbf{Q} \cdot \mathbf{K}^\top}{\sqrt{d_k}} $$ (Vektoren werden üblicherweise mit Kleinbuchstaben geschrieben (zum Beispiel: q, k, v), Matrizen hingegen mit Großbuchstaben (zum Beispiel: Q, K, V).)
Jetzt zählen die wahren Werte!#
Im nächsten Schritt kommen endlich die Value-Vektoren ins Spiel.
Jetzt entscheidet sich, welche Informationen aus dem Kontext auf welches Token übertragen werden.
Doch bevor wir loslegen, müssen wir noch ein Problem lösen …
Bitte nicht schummeln …#
Wenn wir für jedes Token alle Attention Scores im Satz berücksichtigen, könnte das Modell auch auf Tokens zugreifen, die erst später folgen – und damit Informationen nutzen, die es zu diesem Zeitpunkt eigentlich noch gar nicht kennen dürfte.
Das widerspricht der Idee eines autoregressiven Decoders, der bei der Vorhersage ausschließlich auf frühere Tokens zugreifen darf.
Die Attention-Maske#
Wie verhindern wir diese Schummelei?
Mit einem einfachen Trick: Wir verwenden eine Maske. Dabei werden alle Scores, die sich auf zukünftige Tokens beziehen, ausgeblendet – oder etwas technischer: Sie werden durch −∞ (oder eine sehr große negative Zahl) ersetzt, damit diese Positionen bei der Berechnung komplett ausgeschlossen werden.
Wird anschließend die Gewichtung (Softmax) angewendet, werden diese Positionen automatisch auf null gesetzt – und damit vollständig ignoriert.
Welches Token trägt wie viel bei?#
Mit der Attention-Matrix wissen wir nun, welche Tokens einander Aufmerksamkeit schenken. Doch wie genau beeinflussen diese Scores, welche Merkmale ein Token von anderen übernimmt?
Die zentrale Idee: Tokens erhalten im Kontext nicht nur Aufmerksamkeit, sondern übernehmen auch Merkmale – und zwar aus den Value-Vektoren der Tokens, auf die sie sich fokussieren.
Das Team um Vaswani hat dafür einen eleganten Mechanismus entwickelt:
Man geht zeilenweise durch die Attention-Matrix – also Token für Token – und berechnet für jedes Ziel-Token, welche anderen Tokens in der Zeile wie stark beitragen.
Allerdings: Die rohen Attention-Scores sind noch nicht direkt geeignet zum Rechnen – sie sind nicht skaliert, nicht normiert, und schwer vergleichbar.
Deshalb brauchen wir eine Funktion, die Ordnung in diese Werte bringt mit denen wir zuverlässig gewichten können.
Die Rolle der Softmax-Funktion#
Hier kommt die Softmax-Funktion ins Spiel.
Sie ist eine mathematische Methode, mit der sich eine Liste von Zahlen in relative Gewichtungen umrechnen lässt.
Dabei wird jeder Wert zunächst durch die Exponentialfunktion verstärkt und anschließend so normalisiert, dass alle Ergebnisse zwischen 0 und 1 liegen und ihre Summe genau 1 ergibt.
So entstehen proportionale Gewichtungen: Größere Eingabewerte erhalten mehr Gewicht, kleinere weniger – so wird die Auswahl gezielt auf die relevantesten Tokens gelenkt.
Die Softmax-Funktion liefert uns damit für jedes Token in einer Attention-Zeile genau den Multiplikator, mit dem sein Value-Vektor gewichtet in das Ziel-Token einfließt.
Die Softmax-Werte einer Zeile ergeben immer genau 1 – das garantiert, dass die resultierende Kombination der Value-Vektoren stabil und ausgewogen ist.
$$ \text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}} $$
👉 Probiere aus, wie sich die Softmax-Gewichtungen verändern, wenn du die Score-Werte anpasst:
Das neue Embedding entsteht#
Jetzt haben wir alles beisammen:
- Die Attention-Matrix zeigt, wie stark ein Token auf andere achtet.
- Die Softmax-Funktion wandelt diese Werte in Gewichtungen um.
- Die Value-Vektoren enthalten die Merkmale, die weitergegeben werden.

Nun berechnen wir für jedes Token die gewichtete Summe der Value-Vektoren – mit den Softmax-Werten als Multiplikatoren.
Das Ergebnis ist ein neuer, kontextsensitiver Merkmalsvektor – also das neue Embedding.
Dieser Vektor fasst zusammen, welche Informationen aus dem gesamten Satzkontext für das aktuelle Token wichtig sind.
Die Formel, die gerade die Welt verändert!#
$$ \cancel{\boldsymbol{E = mc^2}} $$
$$ \mathbf{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \mathbf{softmax}\left( \frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d_k}} + \mathbf{M} \right)\mathbf{V} $$
Der gesamte Vorgang der Self-Attention, den wir hier beschrieben haben, wurde von Vaswani und seinem Team in einer einzigen eleganten Formel zusammengefasst.
Alle Hochachtung für diesen genialen Mechanismus – an Vaswani, das gesamte Forschungsteam und natürlich auch an all jene, die zuvor den Weg dafür bereitet haben.
An heutigen Tools wie ChatGPT, Gemini und vielen anderen sehen wir Entwicklungen, die wir noch vor wenigen Jahren für undenkbar gehalten hätten.
Und es ist sehr wahrscheinlich, dass wir schon bald weitere emergente Phänomene erleben werden – Entwicklungen, die unsere heutige Vorstellungskraft nicht nur fordern, sondern weit übersteigen.
Wie geht es nun weiter?#
Mit der Self-Attention haben wir nun ein Embedding erzeugt, das für jedes Token – insbesondere das letzte („schläft“) – den gesamten Kontext berücksichtigt.
Was jetzt noch fehlt: Dieses Embedding muss einem konkreten nächsten Token zugeordnet werden.
Dafür kommt ein weiteres neuronales Netz ins Spiel: ein Feedforward-Layer, der das Embedding weiterverarbeitet – und dabei hilft, logische und semantische Muster zu erkennen.
Am Ende erzeugt ein Decoder eine Wahrscheinlichkeitsverteilung über das Vokabular – und wählt das wahrscheinlichste nächste Token aus.
Wie das funktioniert, sehen wir im nächsten Kapitel.
© 2025 Oskar Kohler. Alle Rechte vorbehalten.Hinweis: Der Text wurde manuell vom Autor verfasst. Stilistische Optimierungen, Übersetzungen sowie einzelne Tabellen, Diagramme und Abbildungen wurden mit Unterstützung von KI-Tools vorgenommen.