
Wie versteht ein Sprachmodell einzelne Wörter?#
Dank des Tokenizers lässt sich ein ursprünglich für den Computer völlig unverständlicher Text in eine Liste von Token-IDs umwandeln – also in Zahlen, die das Sprachmodell intern digital weiterverarbeiten kann.
Sprachmodelle (LLMs) verarbeiten Texte intern ausschließlich auf Basis solcher Tokens.
Hinweis:
Zur besseren Lesbarkeit verwende ich im Folgenden meist den Begriff „Wort“, obwohl technisch stets Tokens gemeint sind.
Doch wie gelingt es einem Sprachmodell (LLM), aus diesen nackten Zahlen die Bedeutung einzelner Wörter zu erkennen – und letztlich den Sinn ganzer Texte zu erfassen?
Wie machen wir Menschen das?#
Stellen wir uns das Wort „Katze“ vor. Für uns ist es weit mehr als eine Reihe von Buchstaben: Wir verbinden damit sofort Vorstellungen wie weiches Fell, flauschige Ohren, große Augen und schnurrende Laute. Zudem wissen wir aus eigener Erfahrung oder Geschichten, dass Katzen gerne Mäuse jagen, viel schlafen – und mit Hunden nicht immer gut auskommen.

Ein LLM wie ChatGPT versucht genau diese Zusammenhänge ebenfalls abzubilden – aber auf statistische Weise.
Lernen aus Texten: Merkmale ohne Etikett#
Sprachmodelle können die Welt noch nicht selbst beobachten. Sie haben keine Sinne und können daher keine eigenen Erfahrungen sammeln. Stattdessen lernen sie ausschließlich aus Texten – aus zig Milliarden Wörtern, gesammelt aus Wikipedia-Artikeln, Büchern, Foren, Webseiten und vielen anderen Quellen.
Wir haben bereits gesehen, dass neuronale Netze wahre Meister darin sind, komplexe Muster zu erkennen. Beim Training erkennt das Modell typische Muster und Zusammenhänge: dass „Katze“ häufig gemeinsam mit Begriffen wie „schnurrt“, „flauschig“, „Maus“ oder „Tier“ vorkommt.
Aus dieser statistischen Häufigkeit leitet es typische Eigenschaften ab – etwa dass eine Katze oft als weich, klein, Haustier oder verspielt beschrieben wird.
Diese Eigenschaften nennt man latente Merkmale (engl. latent Features) – weil sie nicht direkt benannt oder beschriftet sind. Das Modell vergibt keine festen Etiketten wie „hat Fell“ oder „jagt Mäuse“, sondern entdeckt solche Muster eigenständig auf Basis der Häufigkeit und des Kontexts im Text.
Ähnlich wie bei neuronalen Netzen zur Bilderkennung, bei denen man nicht exakt sagen kann, welche Kante oder welcher Bogen eine „6“ erkennen lässt, lassen sich auch diese Merkmale im Sprachmodell nicht direkt ablesen. Wir wissen nicht, welche intern erkannten Eigenschaften genau für eine „Katze“ stehen – aber das Modell lernt sie aus dem statistischen Zusammenhang der Sprache.
LLMs erkennen eine Vielzahl an Merkmalen – bei GPT-3.5 sind es 12.288 latente Merkmale, auch Dimensionen genannt.
Jedes Wort wird durch diese 12.288 Merkmale beschrieben – das bildet die Grundlage für seine semantische Bedeutung im Modell.
Noch einmal zur Erinnerung: Die Merkmale (Dimensionen) sind abstrakt und für uns nicht direkt interpretierbar.
Vielleicht steht eines davon für etwas wie „flauschig“ – doch diese Bedeutungen sind nicht benannt, sondern entstehen automatisch beim Training des Modells.
Wir Menschen können nur mit bestimmten Analyseverfahren vermuten, welche Eigenschaften sie repräsentieren.
Illustrativ – reale Merkmale sind abstrakt und unbenannt
Dimension Merkmal Beschreibung 1 flauschig / weich Typisches Gefühl des Fells 2 Haustier Wird oft in Haushalten gehalten … … … 12.287 schnurrt Lautäußerung bei Wohlbefinden 12.288 Konflikt mit Hunden Typisches Feindbild in Erzählungen
Jedes einzelne Wort wird als eine Liste von Zahlen dargestellt, zum Beispiel:
[0.12, -0.98, 1.57, 0.03, ..., -0.44]
Jede dieser Zahlen steht für den Wert eines Merkmals (einer Dimension).
Diese Liste von Zahlen nennt man in der Mathematik einen Vektor – in der KI meist ein Embedding, also ein Vektor, der die Bedeutung eines Wortes beschreibt.
Der Merkmalsraum – Bedeutung in Zahlen#
Jedes einzelne Wort im Text wird geometrisch in einen Merkmalsraum (engl. Embedding Space) eingetragen, der seine semantische Bedeutung repräsentiert.
Dieser Vektor, der die Position im Merkmalsraum festlegt und damit die Bedeutung des Worts beschreibt, wird Embedding genannt.
Wörter mit ähnlicher Bedeutung liegen in diesem Raum näher beieinander.
Wir Menschen kennen Räume typischerweise in drei Dimensionen – mit den Achsen Breite, Länge und Höhe.
Der Merkmalsraum in einem Sprachmodell wie GPT-3.5 hat jedoch 12.288 Dimensionen.
Jede dieser Achsen repräsentiert ein latentes Merkmal, das die Bedeutung des Wortes mitbestimmt.
Die Illustration zeigt eine vereinfachte Darstellung von acht Dimensionen eines Embeddings.
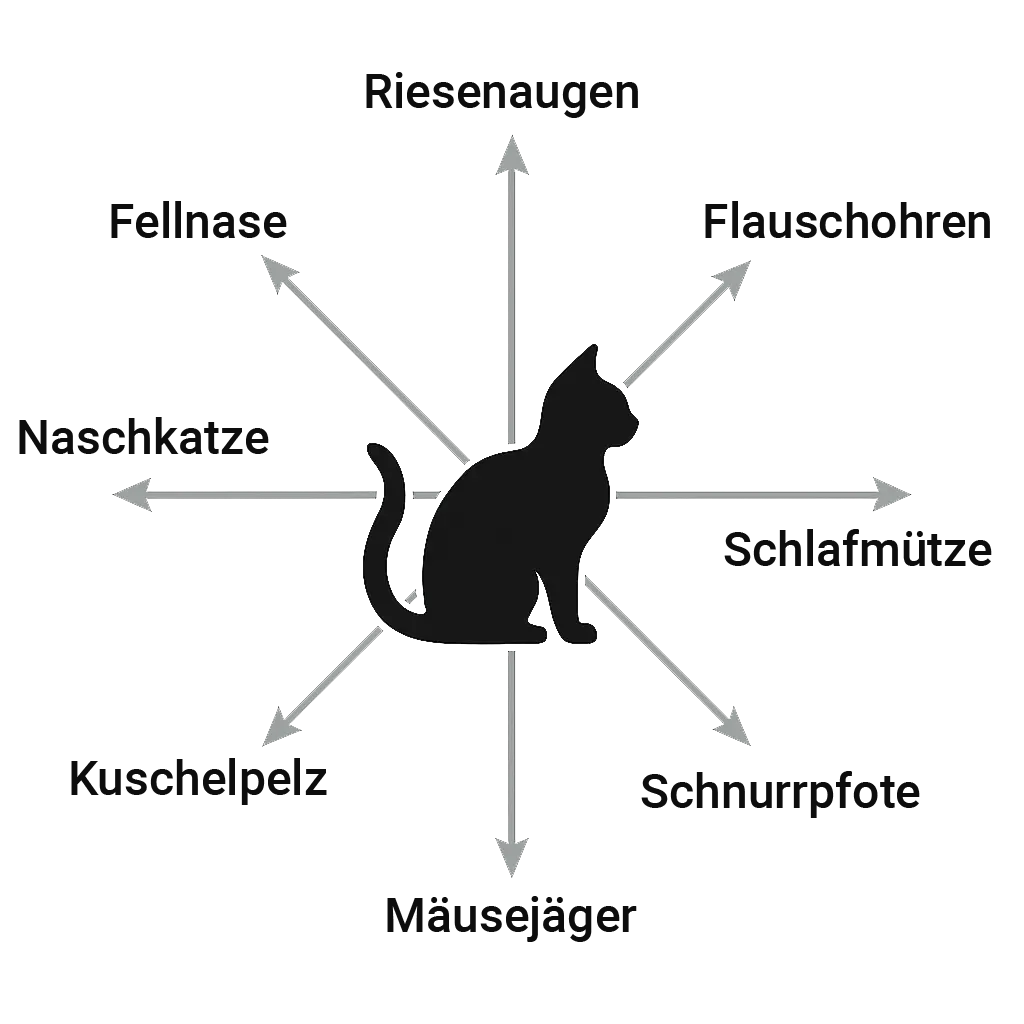
Das ist nicht nur eine Metapher zur besseren visuellen Vorstellung – der Merkmalsraum wird mathematisch tatsächlich als geometrischer Raum abgebildet.
Worte mit ähnlichen Merkmalen – etwa Katze, Hund oder Haustier – gruppieren sich in einer Region des Merkmalsraums, während Begriffe wie Auto, Fahrrad oder Lkw sich in einer anderen Region konzentrieren.
Im geometrischen Vektorraum bilden sich solche semantisch verwandten Begriffe typischerweise zu Clustern (Gruppen).
Je näher zwei Wörter im Raum beieinander liegen, desto ähnlicher sind sie sich inhaltlich bzw. semantisch.
Die Abbildung zeigt eine dreidimensionale Darstellung semantischer Wortbeziehungen.
Ähnliche Begriffe gruppieren sich zu erkennbaren Clustern:
Links sammeln sich typische Haustiere wie Hund, Kaninchen und Meerschweinchen in enger Nachbarschaft.
Etwas abseits thront die Katze auf ihrem eigenen Platz: selbstständig, aber thematisch verwandt.
In der Mitte befindet sich die Transportbox – eine neutrale Verbindung zwischen Tier- und Fahrzeugwelt.
Rechts davon formieren sich zwei weitere Cluster:
Leichte Fahrzeuge wie Fahrrad und Motorrad – und weiter außen schwere Fahrzeuge wie Auto und LKW.
Die räumliche Anordnung ist – wie wir bereits wissen – kein Zufall:
Sie ergibt sich aus den statistischen Mustern, die Sprachmodelle aus Milliarden Wörtern erkennen
Je näher sich Begriffe im Raum befinden, desto stärker ähneln sie sich in Bedeutung und Verwendung.
Ein bekanntes Beispiel veranschaulicht dies: Der Vektorunterschied zwischen „Frau“ und „Mann“ ist ähnlich dem zwischen „Königin“ und „König“, was auf das Merkmal Geschlecht hinweist. Ebenso ist der Unterschied zwischen „car“ und „cars“ vergleichbar mit dem zwischen „dog“ und „dogs“ – das zeigt, dass auch der Unterschied zwischen Einzahl und Mehrzahl im Vektorraum abgebildet wird.
So entsteht aus Sprache ein intuitives, visuell greifbares Landschaftsbild – mit Clustern und Untergruppen.
Wie ähnlich sind zwei Wörter?#
Klassische Embedding-Modelle wie Word2Vec, GloVe oder FastText, aber auch moderne Transformer-Modelle, messen semantische Ähnlichkeit anhand der räumlichen Nähe von Wortvektoren im Embedding Space.
Wörter mit ähnlichem Kontext liegen näher beieinander – unabhängig von Grammatik oder Satzstruktur.
Grundlegend gibt es drei Möglichkeiten, die räumliche Nähe zu messen:
- Euklidische Distanz
Dabei wird der geometrische Abstand zwischen zwei Embeddings über alle Dimensionen berechnet.
Anschaulich entspricht das der „geraden Linie“ zwischen zwei Punkten im Vektorraum.
Für alle, die es mathematisch mögen:
Die euklidische Distanz ist einfach die Länge der Geraden zwischen zwei Punkten, berechnet nach dem Satz des Pythagoras.
Als Beispiel gilt für 3 Dimensionen: $$ d(\mathbf{x}, \mathbf{y}) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + (x_3 - y_3)^2} $$
In der allgemeinen Form für (n) Dimensionen schreibt man kompakter:
$$ d(\mathbf{x}, \mathbf{y}) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2} $$
- Skalares Produkt (Dot-Produkt)
Die Ähnlichkeit von Wörtern lässt sich auch über den Winkel und die Länge der Vektoren ihrer Embeddings verstehen.
Man kann sich das so vorstellen: Je kleiner der Winkel zwischen den Vektoren zweier Wörter ist, desto ähnlicher sind ihre Bedeutungen.
Für alle, die es wieder mathematisch mögen:
Man multipliziert die einzelnen Komponenten (Hadamard-Produkt) und summiert anschließend die Ergebnisse.
So entsteht ein einzelner Wert, der die semantische Ähnlichkeit ausdrückt.
- nahe 0 → kaum Ähnlichkeit
- positiv → semantisch ähnlich
- negativ → eher gegensätzlich
$$ \mathbf{x} \cdot \mathbf{y} = \sum_{i=1}^{n} x_i , y_i $$
- Kosinus-Ähnlichkeit
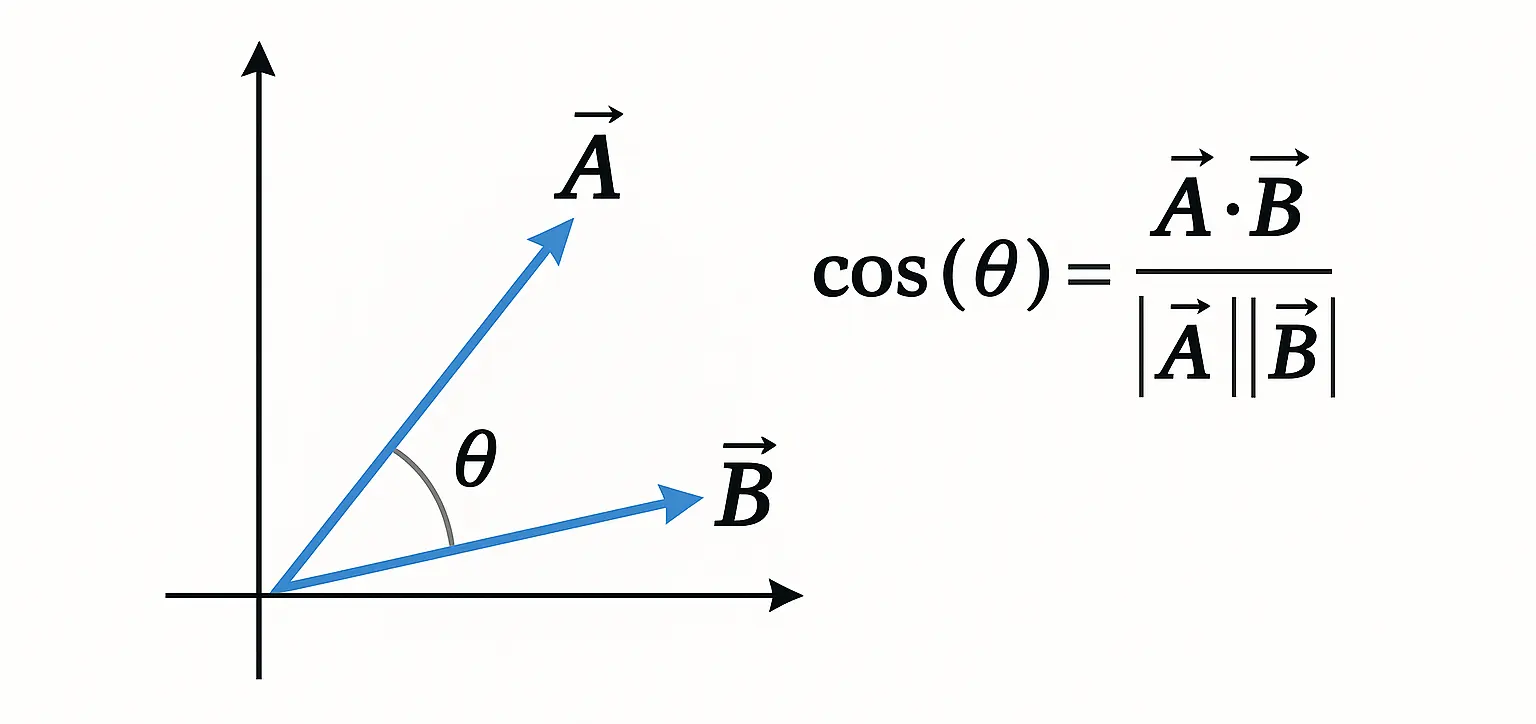
Die Kosinus-Ähnlichkeit geht noch einen Schritt weiter und ist ein normalisiertes Skalarprodukt.
Das bedeutet: Es wird nur der Winkel zwischen den Vektoren betrachtet, unabhängig von ihrer Länge.
Das Ergebnis liegt immer zwischen –1 und 1.
Wie auch bei den anderen Verfahren fließen alle Dimensionen der Embeddings in die Berechnung ein.
Für alle Matheliebhaber:
$$ \cos(\theta) = \frac{ \vec{A} \cdot \vec{B} }{ | \vec{A} | \cdot | \vec{B} | } $$
Die Formel misst, wie ähnlich zwei Wort-Embeddings im semantischen Raum ausgerichtet sind.
- Im Zähler steht ihr Skalarprodukt – also wie stark sie in die gleiche Richtung zeigen.
- Im Nenner das Produkt ihrer Längen – wodurch die Werte normiert werden.
Das Ergebnis liegt zwischen –1 und 1:
Je näher an 1, desto ähnlicher sind die Bedeutungen der Wörter.
Zusammenfassung#
| Verfahren | Idee | Wertebereich | Typischer Einsatz |
|---|---|---|---|
| Euklidische Distanz | Geometrischer Abstand im Raum | 0 → ∞ | Clustering, Abstandsmaße |
| Skalares Produkt | Berücksichtigt Winkel und Vektorlängen | –∞ → +∞ | Attention, Ranking, Scores |
| Kosinus-Ähnlichkeit | Winkel zwischen Vektoren (normiert) | –1 → +1 | Semantische Suche, Retrieval |
Das Prinzip der Vektorähnlichkeit wird auch in modernen KI-Anwendungen genutzt – etwa bei der semantischen Suche, bei der Begriffe nicht nur wörtlich, sondern über ihre Bedeutung verglichen werden.
Auch Sprachmodelle verwenden es, um aus großen Textmengen passende Inhalte zu finden und weiterzuverarbeiten.
Moderne LLMs wie ChatGPT gehen allerdings deutlich weiter: Sie vergleichen nicht nur die semantische Nähe von Wörtern, sondern berücksichtigen zusätzlich auch Grammatik, Satzstruktur und Kontext.
Wie das genau funktioniert, schauen wir uns in den nächsten Abschnitten an.
Mehr als Sprache: Multimodale Embeddings#
Embeddings sind längst nicht mehr “nur” auf Sprache beschränkt.
Neben Text und Tokens lassen sich auch andere Medientypen in Vektoren übersetzen – etwa Bilder, Audio oder sogar Video.
So können KI-Modelle Bedeutungen nicht nur sprachlich, sondern auch visuell und akustisch erfassen.
Die bisher besprochenen Embeddings beziehen sich auf Wort-Embeddings (genauer gesagt Token-Embeddings).
Doch die neuen Modelle von OpenAI, Anthropic, IBM, Meta und anderen sind multimodale Foundation-Modelle:
Sie verstehen nicht nur Text, sondern auch Bilder und Audio.
Das Grundprinzip bleibt dabei gleich:
- Texte zerlegen sie in Tokens,
- Bilder in kleine Bildausschnitte (Patches),
- Audio in kurze Zeitfenster (Samples).
Aus diesen Fragmenten erzeugen die Modelle Vektoren (Embeddings) und verankern sie in semantischen Räumen.
Dabei gibt es zwei Ansätze:
- ein gemeinsamer Embedding-Space für alle Modalitäten,
- oder separate Räume, die durch das Training so aufeinander abgestimmt werden, dass sie miteinander kompatibel sind und sich direkt vergleichen lassen.
So können die Modelle crossmodal arbeiten – ein Bild mit einer Textbeschreibung abgleichen oder ein Geräusch mit einem geschriebenen Begriff verknüpfen.
Auf diese Weise entsteht ein multimediales Verständnis von Inhalten.
Ein einfaches Beispiel macht das greifbar:
- Text → Bild: Die Eingabe „eine Katze in einer Transportbox“ liefert in einer Bilddatenbank genau die passenden Bilder.
- Bild → Text: Ein Foto der gleichen Szene führt zu einer automatisch generierten Bildbeschreibung in Worten.
So verknüpfen multimodale Foundation-Modelle Inhalte in beiden Richtungen und schaffen Verbindungen zwischen Text, Bild und Audio.
© 2025 Oskar Kohler. Alle Rechte vorbehalten.Hinweis: Der Text wurde manuell vom Autor verfasst. Stilistische Optimierungen, Übersetzungen sowie einzelne Tabellen, Diagramme und Abbildungen wurden mit Unterstützung von KI-Tools vorgenommen.